盛最多水的容器
- swfoodt
- Leet code , 每日一题
- June 3, 2022
内容目录
11. 盛最多水的容器
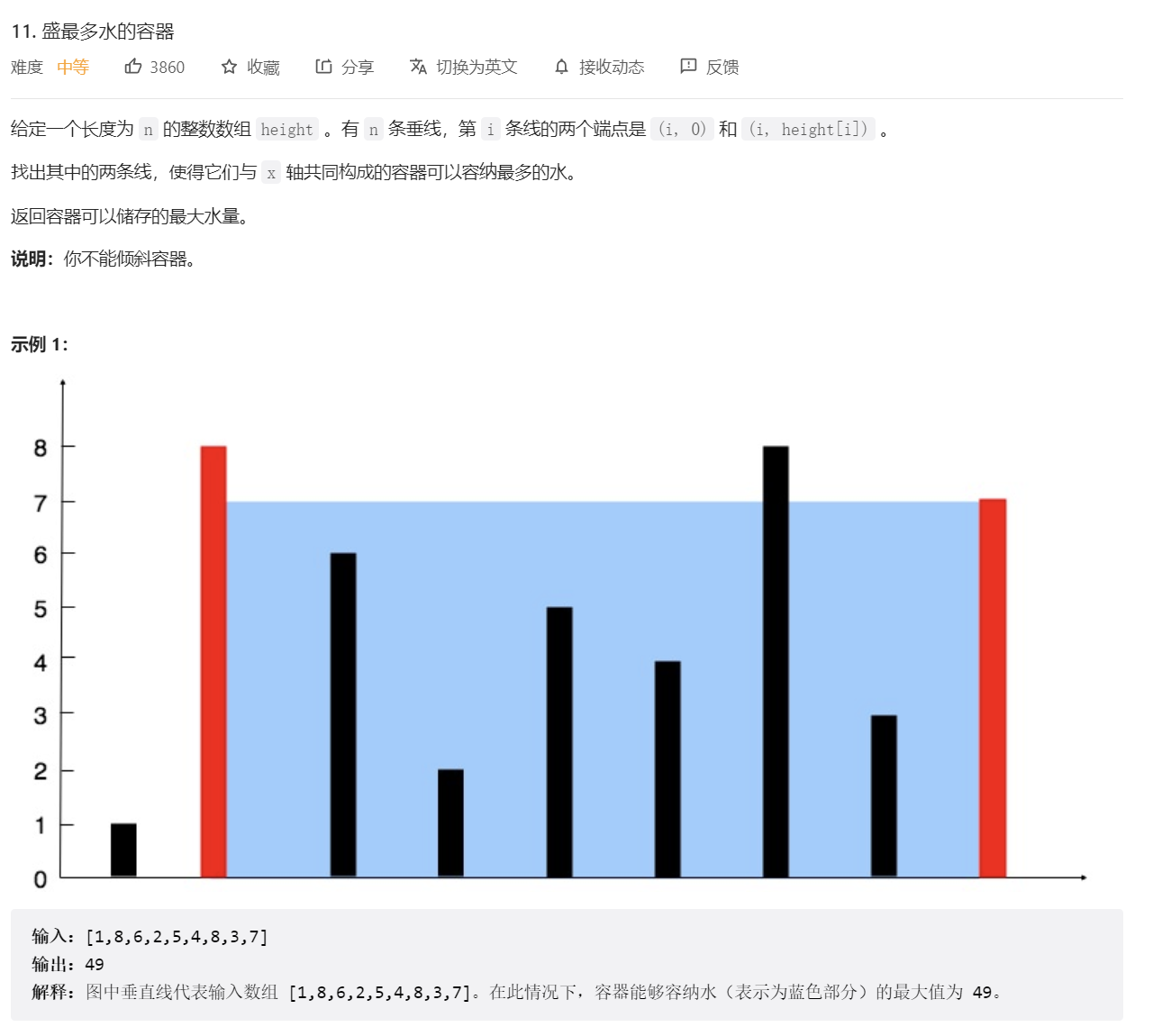
题目分析
刚开始接触到这个题目的时候可能会想着只要将所有情况遍历一遍,先是 i 为左桶沿的所有情况,然后 i+1 ,i+2… 但是这种做法显然不是最优解。不如我们换一种遍历的想法。
刚才我们是想要将所有值都作为桶的一边遍历一遍。要是我们遍历桶底长度呢。
桶底的长度最大值为数组的长度,也就是将数组两端的值作为桶的两边,这样从最大遍历到最小时间复杂度为 O(n),每次将桶底长度减一,也就是将数组的两端向中间移动一位。选择移动哪一边呢? 显然是选择较短的那一边。
这种方法是典型的双指针法。
逐步实现:
首先我们需要两个指针指向数组的两端:
/**
* @param {number[]} height
* @return {number}
*/
var maxArea = function (height) {
let r = height.length - 1; // 右指针
let l = 0; // 左指针
};
然后开始遍历数组,每次遍历都将桶底长度减一,并且判断当前的面积是否大于之前的最大面积:
/**
* @param {number[]} height
* @return {number}
*/
var maxArea = function (height) {
let r = height.length - 1; // 右指针
let l = 0; // 左指针
let max = 0; // 最大面积
for (let i = 0; i < height.length; i++) {
// 遍历数组
let a = Math.min(height[l], height[r]); //最小桶边
let s = a * (r - l); // 面积
height[l] > height[r] ? r-- : l++; // 移动指针
max = Math.max(max, s); // 更新最大面积
}
return max;
};
总结
这一题无论是题目的难度,还是最终代码实现的难度,都不高。但是前提是能够想到双指针法的方法,这是一种常见且高效的解题思路。